
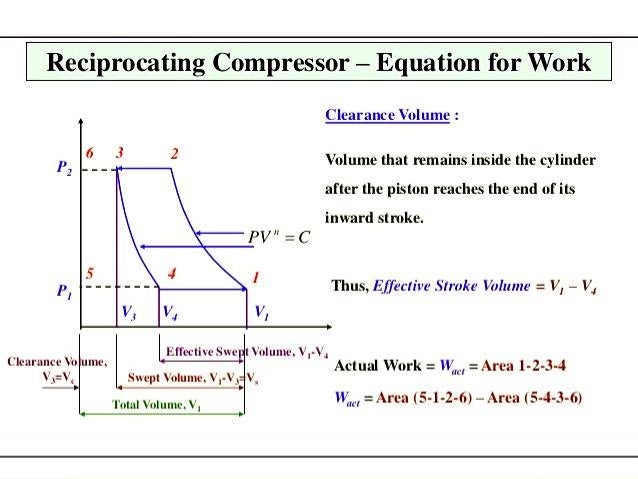
The external pressure is constant in our problem, therefore, the differential equation can be solved easily. The pressure of the gas is continuously changing, therefore, we would need to obtain a function/equation which describes how the pressure changes with volume to solve the differential equation. Let us compare both the ways of calculating work. Hookes Law provides us with an equation that can be used to calculate the exact magnitude of the force required to compress or stretch a spring by some. Work is done when a force moves an object in the direction of the force Work (J) force (N) x distance moved in the direction of the force (m) Energy is the. In the process, the pressure of the gas is continuously changing.Īny work that is done by the gas is as good as the work done by the external pressure in the opposite direction (can be negative work). In the following problem, the gas is doing work by pushing the piston (assume outwards).
See Answer Diagram A Answer: W (100 N) (5 m) cos(0 degrees) 500 J. Although we often hear people talking about energy consumption, energy is never really destroyed. Apply the work equation to determine the amount of work done by the applied force in each of the three situations described below. Energy can be stored and measured in many forms. Energy is a measurement of the ability of something to do work. We consider whichever pressure is most appropriate in a given situation. Though it is often used quite loosely, it does have a very specific physical meaning. Honestly, it does not matter which pressure you consider because work done by the gas is equal to the work done by the external pressure numerically (conservation of energy).

Here is a link to an article I wrote that explains the difference between reversible and irreversible gas expansion (and compression work) in terms of the close analogy to a mechanical spring-damper system: So, in an irreversible process, the work done by the gas on the surroundings is given by $$W=\int$$ Orient the rod so it aligns with the (x)-axis, with the left end of the rod at (xa) and the right end of the rod at (xb) (Figure. We can use integration to develop a formula for calculating mass based on a density function.
#Equation used in workdone download#
This equation is derived by simply dividing both sides of the equation for work done by the time taken. For more audio journalism and storytelling, download New York Times Audio, a new iOS app available for news subscribers. Calculate the work done by a variable force acting along a line. SI Unit: Watt (W) Power can also be defined in terms of force and velocity. Formula: Power Work done (J) / Time taken (s) Simplified formula: P W.D. The force per unit area at the piston face (where the work is being done) $\sigma_f$ is also affected by viscous stresses (which are not present if the process is reversible). Power is mathematically defined as the work done divided by the time taken. If the process is irreversible, the pressure of the gas within the cylinder is not uniform, and varies with spatial location.


 0 kommentar(er)
0 kommentar(er)
